Transformer架构解码器详解

概述

Transformer 的编码器是整个模型的“理解中枢”，它就像一位专业的文本分析师，专门负责 深度解读输入序列（比如一句话或一段文字），并为其中的每个词元（Token）精心制作一份富含上下文信息的“语义身份证”。

这些精心加工的语义表示，将成为解码器生成目标序列（如翻译结果）时最可靠的参考蓝图。🖼️

编码器的设计采用了一种优雅的堆叠结构：它由多个结构完全相同的编码器层（Encoder Layer）叠加而成。你可以把它想象成一座多层信号处理塔——每一层都对输入信息进行一轮提炼和深化，让理解变得更加透彻。

每个编码器层：都像一位“双重身份”的专家 👨🔬👩🔬

每一层都有两个核心职责，分别由两个专业子层担当：

1. 自注意力子层：建立全局关联的“社交网络大师”​ 🤝

这个子层的作用是让序列中的每个位置都能与其他所有位置“对话”。通过计算词与词之间的注意力权重，它能够敏锐地捕捉长距离依赖关系，例如：

代词“它”应该指向前文的哪个名词？

“虽然……但是”之间的逻辑转折在哪里？

哪些词在语义上属于同一个意群？

🌟 简单说：它负责回答“谁和谁有关？关系有多强？”

2. 前馈神经网络子层：深度加工的“特征精炼师”​ 🔧

在自注意力层理清关系之后，这个子层会对每个位置的表示进行独立的非线性变换。它就像为每个词配备了一个私人定制的小型神经网络，专门负责：

提取更深层的特征

增强模型的表达能力

融合从全局关系中获得的洞察

🌟 简单说：它负责回答“基于这些关系，每个词现在应该是什么样子？”

自注意力层

自注意力机制是 Transformer 模型的灵魂组件。它的核心使命是：让序列中的每个位置都能与其他所有位置建立联系，从而生成一个融合了全局上下文的全新表示。

因为它的工作方式完全内向——就像一个人自我反思时，只参考自己过去的经历和想法。模型在计算每个词的表示时，所依据的信息全部来自输入序列本身，不依赖任何外部序列。这就是“自”（Self）的含义

自注意力如何工作

每个词进入注意力机制时，会领到三张不同的“身份卡”：

自注意力的核心思想是：每个位置用自身的 Query 向量，与整个序列中所有位置的 Key 向量进行相关性计算，从而得到注意力权重，并据此对对应的 Value 向量加权汇总，形成新的表示。

三个向量的计算公式如下：

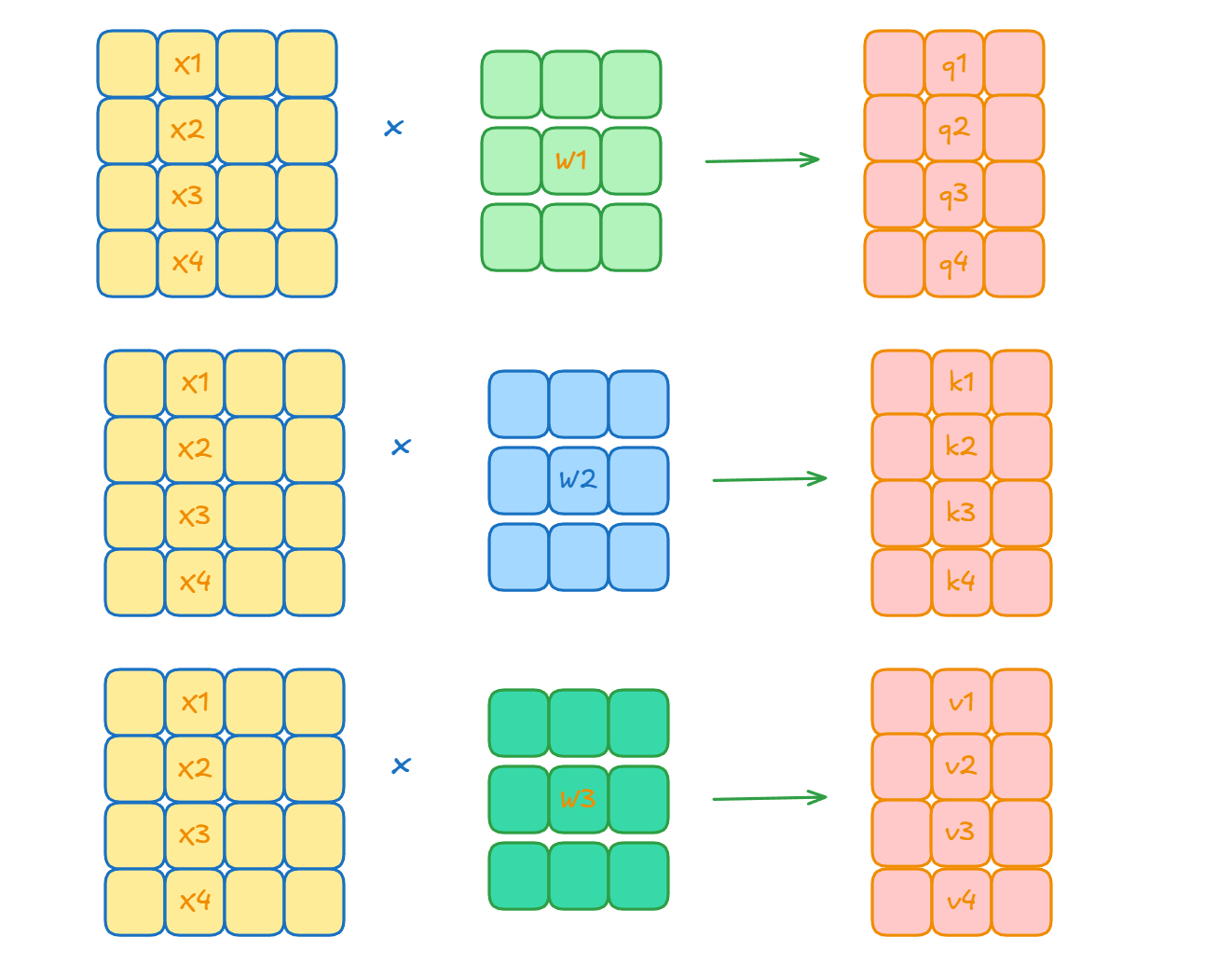
其中w1 w2 w3都是可学习的参数矩阵

计算位置间相关性

完成 Query、Key、Value 向量的生成后，模型会使用每个位置的 Query 向量与所有位置的 Key 向量进行相关性评分。

计算方式：相似度 = (Query · Key) / √(Key的维度)

这个分数越大，表示其应该更加关注这个位置的信息。

为什么除以√(维度)？​

因为在高维空间中，点积结果容易过大，会导致后续的softmax函数“饱和”（梯度消失），这个缩放操作能让训练更稳定。

矩阵版一次搞定：

实际操作中，模型把所有词的Query堆成矩阵Q，所有Key堆成矩阵K，一次性算出所有配对分数：

分数矩阵 = Q × Kᵀ / √dk

计算注意力权重

得到的原始分数还不能直接用——我们需要让每个词对其他所有词的关注度加起来等于100%。

这时候就用上了 softmax 函数：

• 对每个词的分数行进行softmax
• 高分更高，低分更低（突出重要关系）
• 所有分数变为0-1之间，且总和为1

结果：得到清晰的注意力权重矩阵，直观显示“谁应该关注谁多少”。

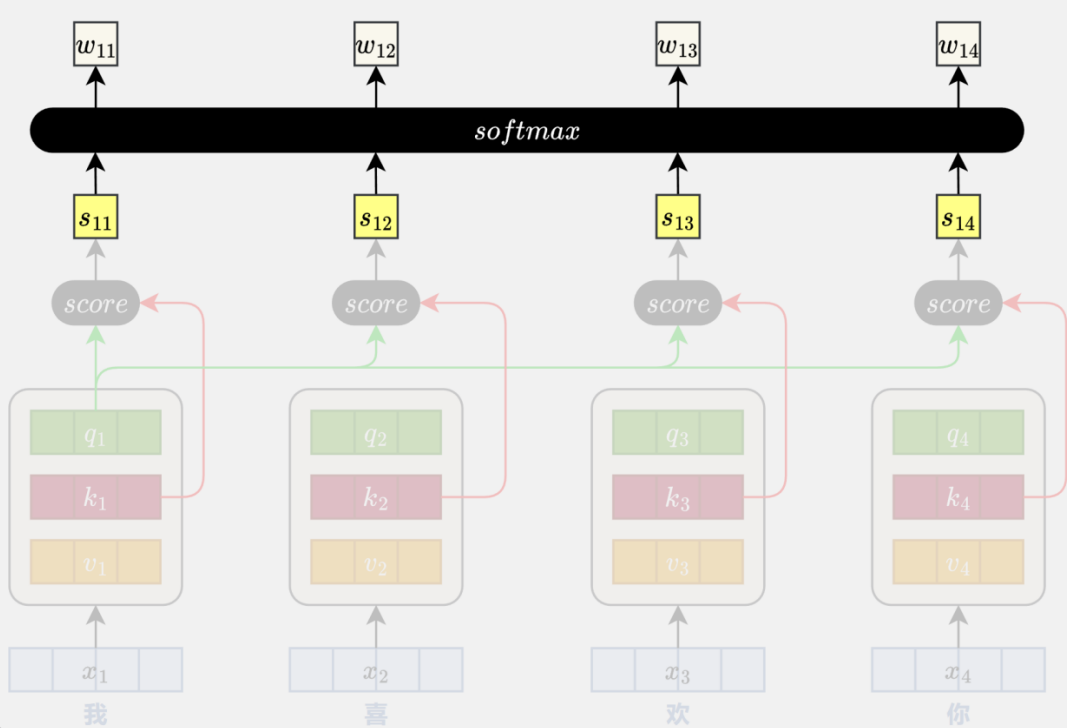
加权汇总：按关注度融合信息

每个词按照上一步算出的“关注度”，对所有词的 Value 卡（实际信息）进行加权求和

新表示 = ∑(注意力权重 × 对应的Value)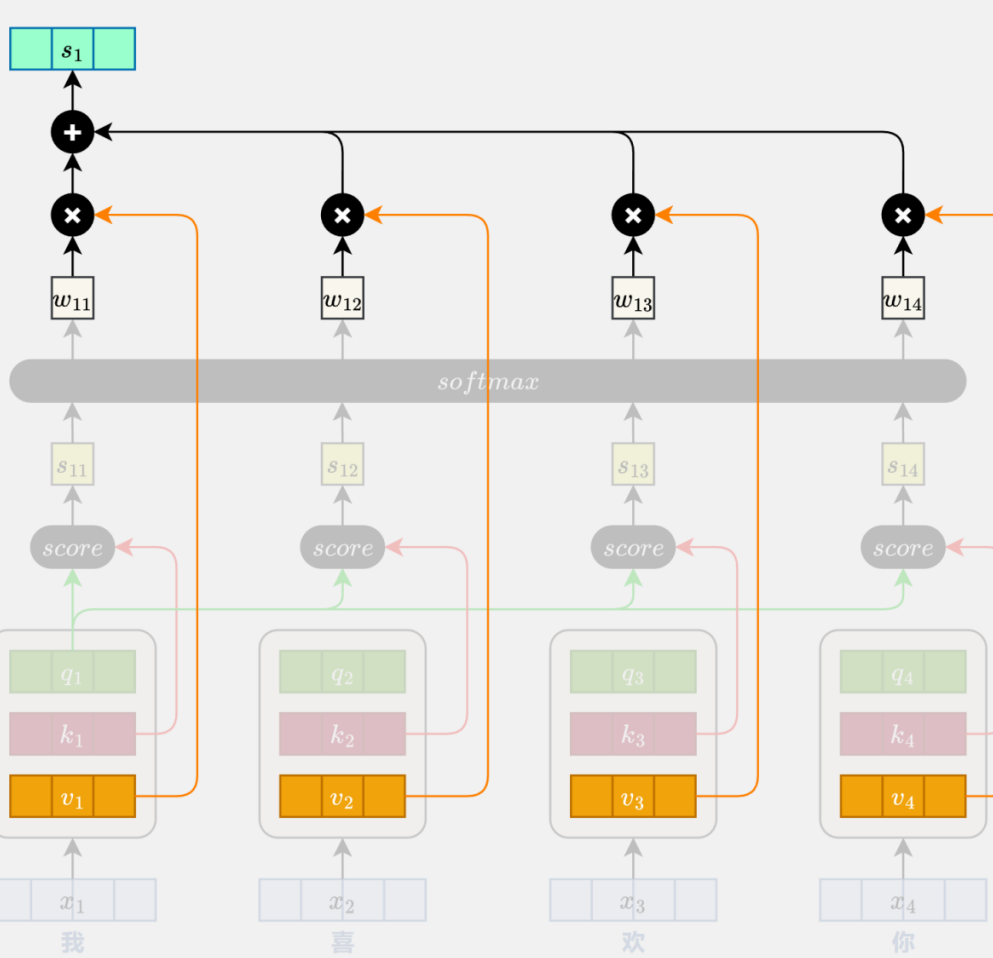

多头自注意力机制

多头自注意力机制解决了单一注意力在理解复杂语句时的局限性，通过多个并行的注意力头，从不同维度捕捉语义关系。

核心动机

考虑句子：“尽管价格昂贵，但这款手机因其出色的拍照功能而广受好评。”

这句话包含多个层面的语义关系：

• 转折关系：“尽管…但…”的对比结构
• 因果关系：“因…而…”的逻辑连接
• 评价关系：“昂贵”与“广受好评”的情感对比
• 属性关联：“手机”与“拍照功能”的产品特性

单一注意力机制难以同时处理这些复杂的交互关系。

工作原理

设输入序列维度为d，头数为h，每个头的维度为d/h。

第一步：分头投影

将输入向量通过h组不同的线性变换，生成h组独立的Query、Key、Value向量。每组变换关注输入的不同特征维度。

第二步：并行计算注意力

每个头独立计算注意力分数和加权输出：

• 头1可能专注于转折关系的识别
• 头2可能捕捉因果逻辑的连接
• 头3可能分析情感评价的对比
• 头4可能关注产品属性的关联

第三步：融合多视角信息

将所有头的输出拼接，通过一个最终的线性层进行融合，形成综合的语义表示。

前馈神经网络层

在Transformer架构中，前馈神经网络（FFN）​ 是紧随多头注意力之后的“深度加工”环节。如果说注意力机制让模型学会了“如何联系”，那么FFN就让模型懂得了“如何深化”。

简单来说，FFN在做三件事：

1. 独立思考

FFN的特别之处在于，它对序列中的每个位置独立处理。想象一下：

• 注意力机制 = 让所有人开圆桌会议，互相交流
• FFN = 会后每个人回到自己的工位，消化讨论成果，写下自己的深度分析

2. 三步加工

FFN的工作流程很直观：

输入特征 → 扩展维度 → 激活处理 → 压缩输出

具体来说：

• 第一步：用第一个线性层将特征维度放大（通常放大4倍），为深度思考创造空间
• 第二步：通过ReLU激活函数，引入非线性变换，这是模型能够理解复杂语义的关键
• 第三步：用第二个线性层将特征维度压缩回原始大小，得到精炼后的表示

3. 功能定位

在每个Transformer层中，信息的流动是这样配合的：

输入 → [注意力（建立关联）] → [FFN（深化理解）] → 输出

这种“先建立联系，再深度加工”的节奏，是Transformer理解语言的核心策略。

一个标准的 FFN 子层包含两个线性变换和一个非线性激活函数，中间通常使用 ReLU激活。其计算公式如下：

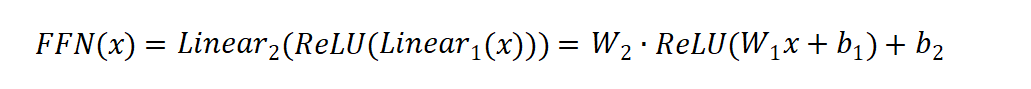
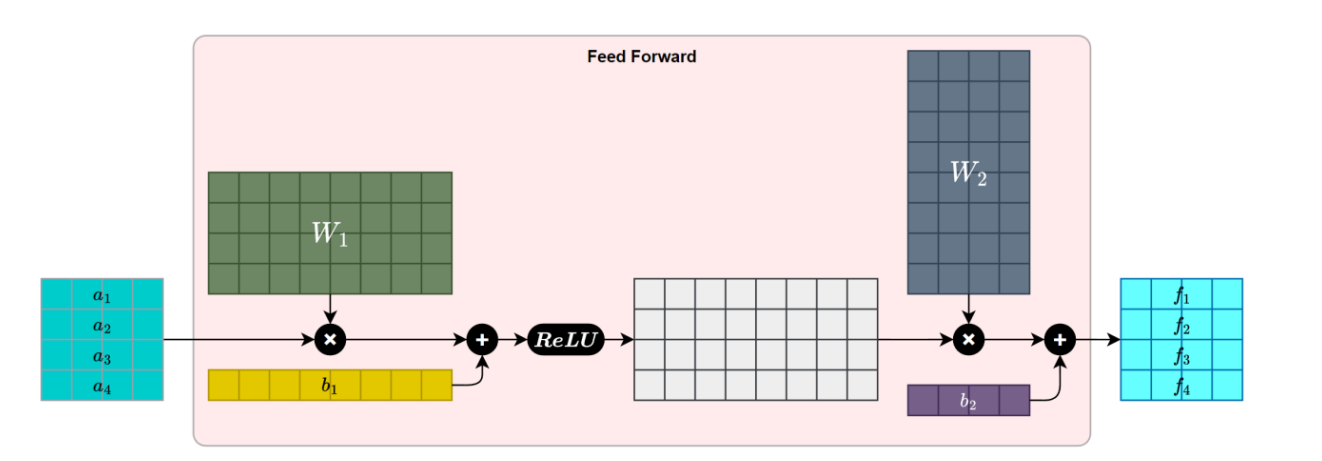
残差连接与层归一化

在Transformer的编码器层中，有两个看似简单却至关重要的组件：残差连接和层归一化。它们就像是模型的“稳定器”，让深度学习网络能够安心堆叠十几层甚至几十层，而不用担心训练崩溃。

残差连接：给梯度开的“绿色通道” 🚀

核心思想

残差连接的思路很直观：让信息“抄近路”。它把子层的输入直接加到输出上，形成一条绕过复杂计算的“捷径”。

数学表达很简单：

输出 = 输入 + 子层处理(输入)

为什么需要它？

想象一个深度网络：

• 第1层：理解单词的基本含义
• 第5层：理解句子结构
• 第10层：理解段落逻辑

如果没有残差连接，第10层要理解段落逻辑，必须等前面9层的信息一点点传递过来，就像传话游戏，传到后面可能已经面目全非了。

残差连接解决了两个关键问题：

1. 梯度消失：在反向传播时，梯度可以直接“走捷径”回传，不会被中间的多层计算稀释
2. 信息保留：原始输入的特征不会在深层处理中丢失，模型可以“回头看”最初的表示

实际效果

在Transformer中，每个子层（自注意力、FFN）都有自己的残差连接：

复制自注意力输出 = 输入 + 自注意力(输入)
FFN输出 = 自注意力输出 + FFN(自注意力输出)

这就像写文章时，你可以在修改稿旁边随时对照原稿，确保不偏离初衷。

层归一化：给特征做的“标准化” 📊

如果说残差连接保证了信息流动，那么层归一化就保证了训练稳定。

它在做什么？

层归一化对每个词的特征向量单独处理：

1. 中心化：让向量的均值为0
2. 标准化：让向量的方差为1
3. 可学习调整：给模型一定的灵活性，可以微调标准化结果

计算公式分四步：

第一步：计算均值和方差

对每个词的特征向量，计算它所有维度的平均值和标准差。

第二步：标准化

标准化值 = (原始值 - 均值) / 标准差

这样处理后，向量就变成了“标准身材”——均值为0，方差为1。

第三步：可学习的调整

最终值 = γ * 标准化值 + β

这里的γ和β是可学习参数，让模型决定“标准身材”是否需要微调。

为什么要归一化？

考虑一个句子中不同的词：

• “apple”可能在某些维度值很大（水果特征强）
• “the”可能在某些维度值很小（语法特征强）

这种差异会导致：

• 训练不稳定（有些值太大，有些太小）
• 收敛困难（梯度来回震荡）

层归一化把它们都拉到同一尺度，就像把不同单位的度量（米、厘米、毫米）都换算成标准单位。

两者的完美配合

在Transformer中，残差连接和层归一化总是结对出现：

每个子层的完整流程
def sublayer_with_norm(x):
# 1. 残差连接：保留原始信息
residual_output = x + sublayer(x)
# 2. 层归一化：稳定训练
normalized_output = LayerNorm(residual_output)
return normalized_output

这种设计的精妙之处在于：

顺序重要：先残差，后归一化

• 残差连接会产生数值范围可能很大的输出
• 层归一化正好把它们“压”回合理范围

分工明确：

• 残差连接：纵向稳定，解决深度问题
• 层归一化：横向稳定，解决特征尺度问题

一句话总结

残差连接让深层Transformer不“失忆”，层归一化让训练过程不“崩溃”。

没有它们，Transformer可能连6层都训练不好，更不用说BERT的12层、24层，或者GPT-3的96层了。这两个简单的组件，是Transformer能够成为“深度学习大力出奇迹”代表作的技术基石之一。

下次当你感叹大模型的能力时，可以想一想：在这些复杂的注意力头和前馈网络背后，正是残差连接和层归一化在默默支撑着整个训练的稳定性。

位置编码：给Transformer装上“顺序感知”的GPS

Transformer模型抛弃了RNN的顺序处理方式，获得了并行计算的超能力，但也因此失去了天然的时序感知。这就好像一个人能同时看见整张拼图的所有碎片，却不知道哪块应该放在哪里。

问题的核心：顺序丢失

考虑这两个句子：

• “猫吃鱼” → 猫是主动者
• “鱼吃猫” → 鱼是主动者

如果只给Transformer看词汇不看顺序，这两个句子对它来说完全一样。这就是Transformer需要位置编码的根本原因。

位置编码的发展历程

方案一：朴素的位置编号（失败尝试）

最初的想法很简单：第一个词标0，第二个标1，第三个标2…

输入 = 词向量 + [0, 1, 2, 3, ...]

问题：数值会越来越大，模型过度关注位置而忽略词义。

方案二：归一化位置（还是不行）

改进一下：把位置缩放到0-1之间

位置5在长度10的句子中：5/10 = 0.5
位置5在长度100的句子中：5/100 = 0.05

新问题：同一个位置在不同句子中编码不同，模型学不会稳定的位置概念。

Transformer的解决方案：正弦余弦编码

最终，Transformer采用了基于三角函数的编码方案：

偶数维度：PE(pos, 2i) = sin(pos / 10000^(2i/d_model))
奇数维度：PE(pos, 2i+1) = cos(pos / 10000^(2i/d_model))

这个设计为什么巧妙？

1. 数值稳定

所有值都在[-1, 1]之间，不会压倒词向量的信息。

2. 位置唯一

位置5在任何句子中都是同一个编码，模型能形成稳定的位置概念。

3. 相对位置可感知

关键在于：位置之间的差值可以通过三角函数公式计算

PE(pos + k) 可以通过 PE(pos) 的线性变换得到

这意味着模型能轻松学会“第3个词在第2个词后面”这种相对位置关系。

4. 可扩展性强

无论句子多长，都能生成对应的位置编码。

可视化理解

想象每个位置编码像一个独特的“指纹”：

• 低频维度（i小的维度）：变化缓慢，捕捉宏观位置
• 高频维度（i大的维度）：变化快速，精确定位

多个不同频率的正弦波叠加，为每个位置创造了独一无二的编码图案。

位置编码的实际使用

在Transformer中，位置编码简单直接地加到词向量上：

最终输入 = 词嵌入向量 + 位置编码向量

模型看到的每个词都带着两个信息：

1. 我是谁（词向量表示的语义）
2. 我在哪（位置编码表示的顺序）

为什么这个方案成功？

对比之前的失败方案：

关键洞察：

正弦余弦编码实现了唯一性与规律性的完美平衡：

• 每个位置编码唯一，但编码之间有数学关系
• 模型既能记住绝对位置，又能推导相对位置
• 不需要训练，节省参数且稳定